Antický svět 

Životopis

Eratosthenés z Kyrény se narodil patrně roku 276 před n.l. v kolonii Kyréné, která leží na území dnešní Libye, ale ve starém Řecku patřila do regionu osídleného řeckými osadníky. Vzdělával se na nejlepším školách své doby - několik let vAthénách a hlavně v Alexandrii, která se pod ochranou dynastie Ptolemaiovců stala útočištěm pro nejlepší učence epochy. Sám Eratosthenés byl žákem učence a básníka Kallimacha, který pocházel ze stejného města a patřil k elitním vzdělancům doby. Mimo jiné to byl právě on, kdo se stal druhým šéfem instituce Múseion a bezpochyby svou vzdělanost v mnoha oborech předal Eratosthenovi.

Z něj se postupem času stal vynikající vědec a badatel, který, jak bylo typické pro onu dobu, se nezabýval jen jednou vědou. Vynikal údajně jako gramatik, literární historik, matematik, astronom, geograf, kartograf, chronolog, etik a básník. Pro jeho všestrannost byl nazýván poněkud vyčítavě Pentathlos, což znamená zápasník v pětiboji. Ten totiž nemusí být ve všem nejlepší, ale stačí mu ve většině disciplín patřit k lepším, aby celkově vyhrál.

Již ve třetím století před n.l. totiž existovala mocná klika zastánců specializace, kteří na Eratosthena shlíželi spatra. Podobně i přezdívka Béta, kterou obdržel, nemusí být nutně kladná. Jak soudí Čestmír Vránek, šlo o přezdívku negativní vzešlou právě od stoupenců specializace, kteří "spatřujíce snad v mnohosti úkolů nebezpečí povrchnosti, mu s jistou povýšeností říkali Béta ve smyslu druhořadý ."Smith na druhou stranu tvrdí , že jeho přízvisko lze vyložit tak, že Eratosthenés byl druhým z velkých antických vzdělanců a písmeno beta tedy jen vystihuje jeho pořadí. Tentýž autor pak píše také to, že dvojka byla číslem jeho pokoje v alexandrijském Múseiu a přezdívka pocházela odsud. Poslední přízvisko, které alexandrijský vědec dostal, je však jednoznačně kladné - jeho obdivovatelé mu říkali"druhý Platón".

Přestože byl Eratosthenés často titulován jako "druhý", je prvním významným geografem starověku. Využil svých znalostí geografie, astronomie a matematiky a spojil tyto vědy do systému matematického nebo též astronomického zeměpisu. Jeho objevy na tomto poli budou vysvětleny v další části článku.

O dobré pozici Eratosthena na dvoře ptolemaiovských králů svědčí to, že byl okolo roku 245 před n.l. jmenován vychovatelem budoucího krále Ptolemaia IV. Filopatera . O pět let později se mu dostalo pocty ještě vyšší, když se po smrti svého učitele Kallimacha stal třetím šéfem alexandrijského Múseia a správcem statisíců svitků s nasbíranými antickými spisy. V této pozici se stal prominentní osobou, mezi jejíž přátelé se řadil, kromě dalších předních vědců doby, i Archimédes.

O pozdních letech života Eratosthena z Kyrény není mnoho známo. Autoři literatury se však shodují v tom, že nedlouho před smrtí oslepnul a svůj život zanedlouho ukončil dobrovolnou smrtí hlady. Mělo se tomu stát roku 194 před n.l. a polyhistor se tak dožil více než osmdesáti let. Přes velké množství materiálu, který napsal, se z jeho díla dochovaly jen zlomky zachycené ve spisech jiných autorů.

Měření zemského obvodu v antickém Řecku
Pravěké představy o ploché Zemi nepřežily výrazněji nástup antického vědeckého myšlení. Za zjištěním kulatosti Země stojí sledování zatmění Měsíce - řečtí, ale také například babylonští nebo egyptští astronomové si byli dobře vědomi toho, že zatmění vzniká působením zemského stínu a že tento stín je kulatý. Proto také zemské těleso musí být kulaté. Prosazení tohoto tvaru Země nebylo ani v antice příliš jednoduché, mnoho velkých osobností vědy věřilo v odlišný tvar - vedle výše zmíněného Tháletova názoru na tvar Země můžeme zmínit například Anaximena, který hovořil o obdélníkovém tvaru tělesa atd.. Přesto se ve 3.století před n.l. mezi učenci více méně ustálil názor, že Země kulatá skutečně je. Snahy o výpočet jejího obvodu brzy následovaly.

První dochovaný odhad nám zanechal Aristoteles, který obvod Země doslova odhadoval na 400 000 stádií, tedy zhruba 65 000 kilometrů. Dalším, kdo zkusil na tomto poli štěstí, byl Archimédes, který hovoří o tom, že někteří spisovatelé mluví o hodnotě obvodu Země 300 000 stádií, což je zhruba 50 000 kilometrů. Nezmiňuje ani autory tohoto odhadu ani jejich metody a Smith tvrdí, že tento odhad je snad starší Eratosthenovou prací. Archimedovy odhady tedy můžeme v podstatě pro nedostatek podkladů zanedbat.

Další tři antické odhady obvodu Země již máme zdokumentované lépe. Autory těchto hypotéz jsou Eratosthenés z Kyrény, Poseidonius z Apameie (135 - 51 před n.l.) a Klaudios Ptolemaios (asi 100 - 178 n.l.). Jejich pokusy o měření obvodu Země jsou již velmi zajímavými hypotézami, které pracovaly s pokročilými nástroji na měření úhlů, ale narážely na problémy při měření vzdáleností. Práce zmíněných vědců také musíme chápat jako řešení typicky akademického problému, který neměl s praxí příliš společného. Jako základní postup používali tito první geodeti určení délky obvodu z délky známého oblouku tělesa. 

Eratosthenés a měření obvodu Země
Z objevů, které se připisují Eratosthenovi z Kyrené, je za nejpozoruhodnější považována jeho metoda měření zemského obvodu. Alexandrijský vědec nemohl při výpočtu obvodu zemského tělesa operovat s poloměrem Země, který nebyl znám. Musel si proto pomoci jinými metodami, konkrétně tzv. úhlovou metodu měření. Smith pak dokonce tvrdí, že "žádný z matematických skutků řeckých astronomů není zajímavější než měření obvodu a poloměru Země Eratosthenem... "

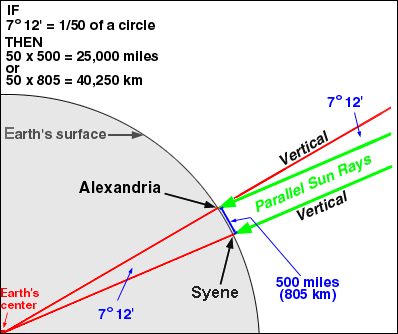Eratosthenův postup je založen na "stanovení vzdálenosti s dvou míst na stejném poledníku, které odpovídá na zemské kouli středový úhel α" . Z takto získaných znalostí by pak bylo již jednoduché odvodit zemský obvod, samozřejmě za předpokladu, že by Země byla ideálně kulatě těleso (což není). Dalším předpokladem je paralelní přístup slunečních paprsků k vybraným stanovištím, což se také neděje zcela přesně.

Eratosthenés se pokusil uvést tuto teorii do praxe tím, že vzal jako oblouk spojnici Syéné (dnešní Asuán) a Alexandrie. Tato vzdálenost měla činit 5000 stádií. Nevíme, jak se k tomuto údaji alexandrijský vědec dostal, nicméně je možné, že byl informován o této vzdálenosti od poslů ptolemaiovské říše, kteří údajně museli zaznamenávat vzdálenosti, které urazili na svých cestách. Zprávy pak patrně byly sbírány v alexandrijské knihovně, odkud je Eratosthenés mohl znát. Rovněž je zmiňována informace o každoročním přeměřování egyptských pozemků po rozlití Nilu z břehů , odkud rovněž bylo snadno možné dozvědět se relativně přesnou vzdálenost. Eratosthenés je rovněž autorem náčrtku mapy Nilu až do Chartúmu. Právě na této řece leží Syéné i Alexandrie. Ať již byl použit jakýkoliv zdroj informací, je zřejmé, že autor této teorie údaj zaokrouhlil a může tedy jít stejně dobře i o údaj tradiční nebo prostě odhadnutý.

Eratosthenés dále předpokládal, že Syéné a Alexandrie leží na stejném poledníku. Tato premisa nebyla nejpřesnější, přestože právě Eratosthenés vytvořil jednu z vůbec prvních map Středomoří položenou na základech matematické kartografie. Rozdíl zeměpisných šířek obou míst podle dnešních souřadnic činí více než tři stupně. 

Eratosthenés dále věděl, že v Syéné v den letního slunovratu (21. 6.) v poledne sluneční paprsky dopadají přímo na dno tamních studní a tělesa, jako jsou obelisky, nevrhají žádný stín. Slunce tím pádem musí být přímo v nadhlavníku (zenitu), což je způsobeno tím, že Syéné leží (téměř) na obratníku Raka a Slunce zde má v době letního slunovratu výšku (nad obzorem) velmi blízkou devadesáti stupňům.

V další fázi musel Eratosthenés srovnat situace v Syéné se situací v Alexandrii. Ta již na obratníku neleží, a proto zde bylo nutné změřit výšku Slunce. Jakých nástrojů k tomu Eratosthenés použil, není přesně známo. Snad šlo o tzv. skafé, kamenné sluneční hodiny vynalezené Aristarchem ze Samu, které umožňovaly měřit úhel dopadu slunečních paprsků. Každopádně Eratosthenés naměřil zenitovou výšku Slunce v poledne v době letního slunovratu o hodnotě 1/50 celkového obvodu, tedy 1/50 z 360°, což je 7,2°.

Eratosthenés tak získal všechny základní komponenty k výpočtu obvodu zemského tělesa: jednu poledníkovou vzdálenost a úhel. Pak již bylo snadné dopočítat celkový obvod Země, který byl brán jako padesátinásobek vzdálenosti pěti tisíc stádií, tedy celkem 250 000 stádií. V poslední fázi pak Eratosthenés pomocí vztahu údajně objeveného Pythagorem, totiž že je "průměr kruhu 3 a 1/7 krát kratší než jeho obvod ", vypočítal také průměr a poloměr zemského tělesa. 

Základní předpoklady této teorie můžeme shrnout do pěti bodů: 
a) Alexandrie a Syéné leží na stejném poledníku 
b) Sluneční paprsky jsou v době svého příchodu k Zemi paralelní 
c) Vzdálenost Alexandrie - Syéné je 5000 stádií 
d) Úhel vytvořený stínem v Alexandrii je roven 1/50 kruhu 
e) Země je dokonale kulatá 

Čistě na bázi teoretické myšlenky je Eratosthenova úhlová metoda měření zemského obvodu bezchybná. V reálu však naráží na některé překážky. Eratosthenés vycházel z nesprávného předpokladu stejné zeměpisné délky Syéné a Alexandrie. Podobně nevěděl nic o tom, že Země není dokonalá koule, nýbrž je na pólech zploštělá, což ostatně dokázaly výpočty Issaca Newtona až v roce 1686.

Dalším problémem výše zmíněných měření je ten fakt, že nemáme představu, v jakých jednotkách Eratosthenés měřil. Samozřejmě šla o stadia, nicméně tyto řecké jednotky měly neméně tvarů než středověká soustava měr a vah odvozených z délek na lidském těle. Tradiční formou starořeckých měr byl stadion o délce přibližně 185 metrů. Při takové hodnotě délkové jednotky by Eratosthenem vypočtený obvod Země činil 46 232 km, což by znamenalo přibližně patnáctiprocentní chybu. Je však také stejně dobře možné, že alexandrijský vědec pracoval s tzv. krátkými stádii (zhruba 157,2 metru) a pak by výsledek činil 39 688 km.

Ať už je však výpočet proveden podle jakýchkoliv měr, Eratosthenův úvodní úsudek byl brilantní. Rovněž to, že většina jeho úvodních předpokladů se nesplnila, může být poněkud zavádějící. Chyby v předpokladech nebyly nijak dramatické a nešlo o chyby v úsudku, nýbrž v přesnosti. Proto i celková chyba Eratosthenova měření, která se může zdát jako dramatická, není na antické poměry rozhodně velká. Slovy Chapmana: "Těžko bychom ovšem mohli popřít skutečnost, že změření Země Eratosthena staví mezi zakladatele geodézie a průkopníka myšlenky, že se teorémy a koncepce geometrie dají aplikovat na skutečný svět a mohou napomoci získání nových vědomostí."

Je nutno také zmínit, že podobnou metodu pro měření obvodu Země použil Poseidonius z Apemeie, který však pro délku oblouku využil spojnice Rhodu a Alexandrie (rovněž o přibližné délce 5000 stadií) a místo výšky Slunce použil výšky hvězdy Canopus. Poseidonius tak došel k celkovému obvodu Země 240 000 stádií, opět však bohužel nevíme, o jaká stadia konkrétně šlo. Jde každopádně o důkaz toho, že na Eratosthenovu práci bylo navazováno již poměrně krátce po jeho smrti. 

Další geografické a astronomické práce 
Vedle odvození obvodu zemského tělesa se Eratosthenés pokusil také o stanovení vzdáleností nejdůležitějších nebeských těles, totiž Slunce a Měsíce, od Země. Vzdálenost Země - Slunce alexandrijský vzdělanec kvantifikoval vzdáleností rovnající se 804 milionům stadií, vzdálenost Země - Měsíc pak 780 000 stádií. Zde měl údajně pracovat s daty získanými z měsíčních zatmění a rovněž zde jsou jeho výsledky až pozoruhodně přesně.

Klaudios Ptolemaios se dále zmiňuje o tom, že Eratosthenés měřil s velkou přesností odchylku zemské osy, kterou kvantifikoval jako 11/83 ze 180°, což je 23°51´15´´. Je však možné, že tento údaj pochází až od Klaudia Ptolemaia, zatímco Eratosthenés pracoval s údajem této hodnoty o velikosti 24° . Rovněž i zde jde o čísla nesmírně přesná, přihlédneme-li k možnostem tehdejších nástrojů.

Eratosthenés dále jako první správně vysvětlil různý průtok Nilu v průběhu roku způsobený periodickými dešti v místě jeho pramenů, podobně jako se správně postavil k otázce hledání pramenů nejdelší africké řeky. Dále sestavil kalendář čítající rovněž přechodné roky nebo katalog hvězd čítající celkem 675 hvězdných objektů. Jeho mapa tehdy známého světa, sahající od Británie až do Cejlon a od Kaspického moře k Etiopii, využívá souřadnicového systému, který dává kartografii vědečtější základ. Pouze pozdější autoři Hipparchos, Strabón a Klaudios Ptolemaios vytvořili v antické době přesnější mapy.

Eratosthénovy matematické práce 
Kromě Eratosthenových prací z oblasti matematického zeměpisu kartografie jsou známé i některé jeho práce matematické. Eratothenés se zabýval klasickým geometrickým problémem zdvojení krychle a liboval si ve zkoumání prvočísel.

Vymyslel metodu, jak nalézt všechna prvočísla menší než zadané přirozené číslo. K vyhledávání prvočísel používal voskové tabulky, na kterých měl napsána všechna přirozená čísla počínaje číslem 2 a konče zvoleným. Nejmenší číslo v tabulce (číslo 2) ponechal a na místa jeho násobků vypálil horkou jehlou dírku. Následujícím číslem v tabulce bylo číslo 3. Toto číslo opět ponechal a odstranil všechny jeho násobky. Dalším nejmenším zbylým číslem bylo 5. Opět jeho násobky odstranil. Takto pokračoval, dokud nedospěl k poslednímu. Po skončení vyhledávání prvočísel vypadala vosková tabulka jako síto. Proto se tato metoda hledání prvočísel v dnešní době označuje názvem Eratosthenovo síto.

Eratosthenovo síto je tedy metoda, kterou lze najít všechna prvočísla menší než námi zvolené přirozené číslo.

Postup: 
- např. do tabulky napíšeme všechna přirozená čísla počínaje číslem 2 do námi zvolené horní meze 
- označíme nejmenší číslo - číslo 2 (prvočíslo) a jeho násobky odstraníme 
- další zbylé nejmenší číslo (číslo 3) je opět prvočíslo a jeho násobky se odstraní 
- následující neškrtnuté číslo je 5, prvočíslo, jehož násobky se odstraní 
- tímto způsobem pokračujeme do doby, dokud za prvočíslo není označeno číslo větší než druhá odmocnina námi zvolené horní meze 
- následují zbylá (neškrtnutá) čísla jsou již všechna prvočísla 

Je jistě patrné, že tato metoda je značně omezená a použitelná jen při relativně malých konečných číslech. Při zvolených číslech řádů tisíců a více je velice časově náročná a ručně téměř nepoužitelná. V dnešní době existuje několik programů na vyhledávání prvočísel právě za pomocí tohoto algoritmu. Přesto i pomocí počítačů tímto algoritmem nenajdeme největší známé prvočíslo, protože takové megaprvočíslo má více jak 4 milióny cifer.

Lokality jmenované ve článku najdete na Mapě antického světa. 

Použité zdroje: 
Brázdil R. a kol: Úvod do studia planety Země, SPN, Praha, 1988. 
Demek J., Pech J., Riedlová M.: Úvod do studia geografie a dějiny geografie, SPN, Praha, 1980. 
Folta J., Šedivý J.: Světonázorové problémy matematiky I, SPN, Praha, 1983. 
Chapman A.: Bohové na nebesích, BB art, Praha, 2003. 
Bahník V [et al.]: Slovník antické kultury, Svoboda, Praha 1974. 
Smith D. E.: History of mathmatics, Volume I, Dover Publications, New York, 1958 
Smith D. E.: History of mathmatics, Volume II, Dover Publications, New York, 1958 
Šedivý J. a kol.: Světonázorová výchova v matematice, Jednota československých matematiků a fyziků, Praha, 1987.

WWW: 
http://turnbull.mcs.st-and.ac.uk/history/Biographies/Eratosthenes.html 
http://mathdl.maa.org/mathDL/1/?pa=content&sa=viewDocument&nodeId=646&pf=1 
http://antika.avonet.cz/article.php?ID=2118 
http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Eratosthenes.html 
http://www.wikipedia.org 
http://www.primzahlen.de/files/theorie/sieb.htm 
http://www.mlahanas.de/Greeks/Greeks.htm 
www.martin-wagenschein.de/K-Kohl/Eratosth.htm